It is now time to prepare the engineering drawings and do the arithmetic and finalize how my complete sculpture will be put together.

This piece began with the idea to build another western sculpture for the Calgary Stampede in 2020. The idea was to create an 1890’s gold mine setting. I thought I could build a scale model ore cart and water wheel. The water wheel would drive the ore crusher.

The electric motor I will use to power the water wheel draws 1.5A at 6V or 9W of power at maximum load. The motor rotates at 12 RPM. As a 12 RPM rotation for a water wheel is a little fast, I will gear the motor further to about 3 RPM. At this speed each revolution of the wheel will take 20 seconds.

To get enough torque or power to raise a heavy ball I need to gear down the water wheel even more. I will use 2 sets of visible brass gears to gear down by 2 and then by 2 again to have my crusher operate at 0.75 RPM, or once every 80 seconds.

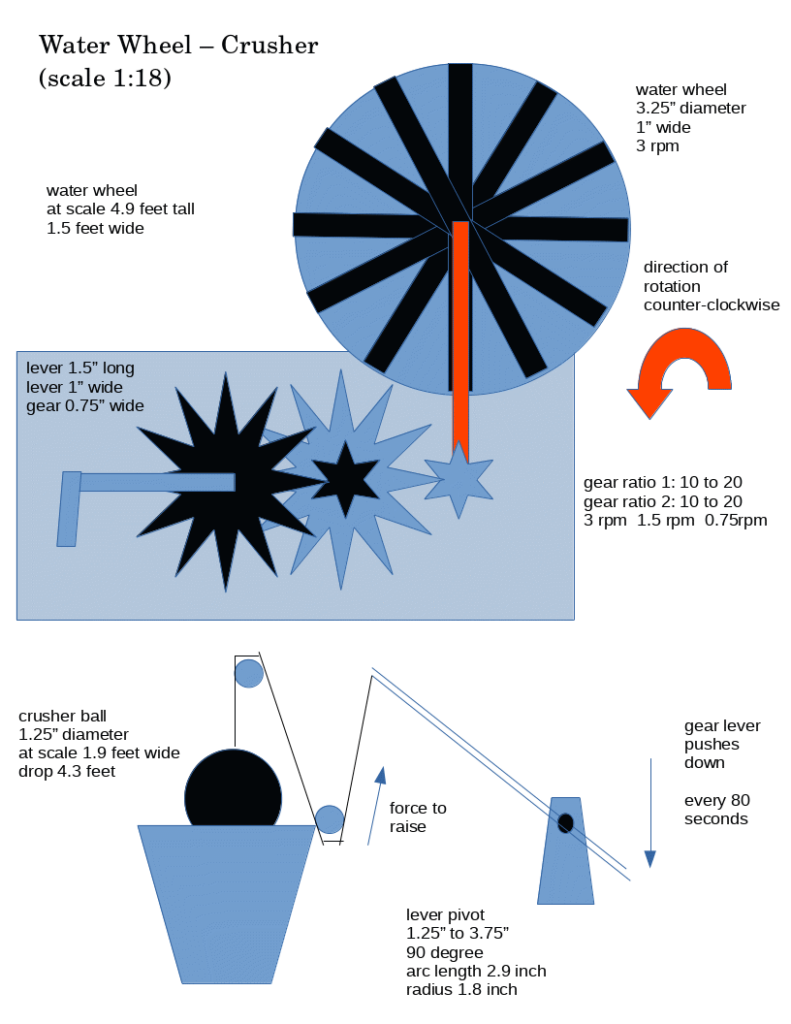
Power (kW) = Torque (N.m) x Speed (RPM) / 9.5488. Converting 9 watts to torque at 0.75 RPM we get 114.6 mNm of maximum torque generated by the motor.

My water wheel will rotate an arm that once each revolution presses down on one end of a lever or see-saw. Pressing down on one end raises the other end, which by a series of pulleys will raise the crusher ball.

Torque (mNm) = mass (g) x 9.8 m/s2 x radius. In my case the lever used to raise the ball 1.8 inches is like a 90 degree pulley with arc of 2.9 inches or a radius of 0.047m. The maximum possible mass is 114.6 mNm / (0.047m * 9.8m/s2) = 248 grams.

My solid cast brass crusher ball weighs about 130 grams. If I assume an overall efficiency of about 0.7 for this Rube Goldberg machine I will hopefully have enough force to make this work. The whole operation should be slow enough and massive enough to appear realistic.

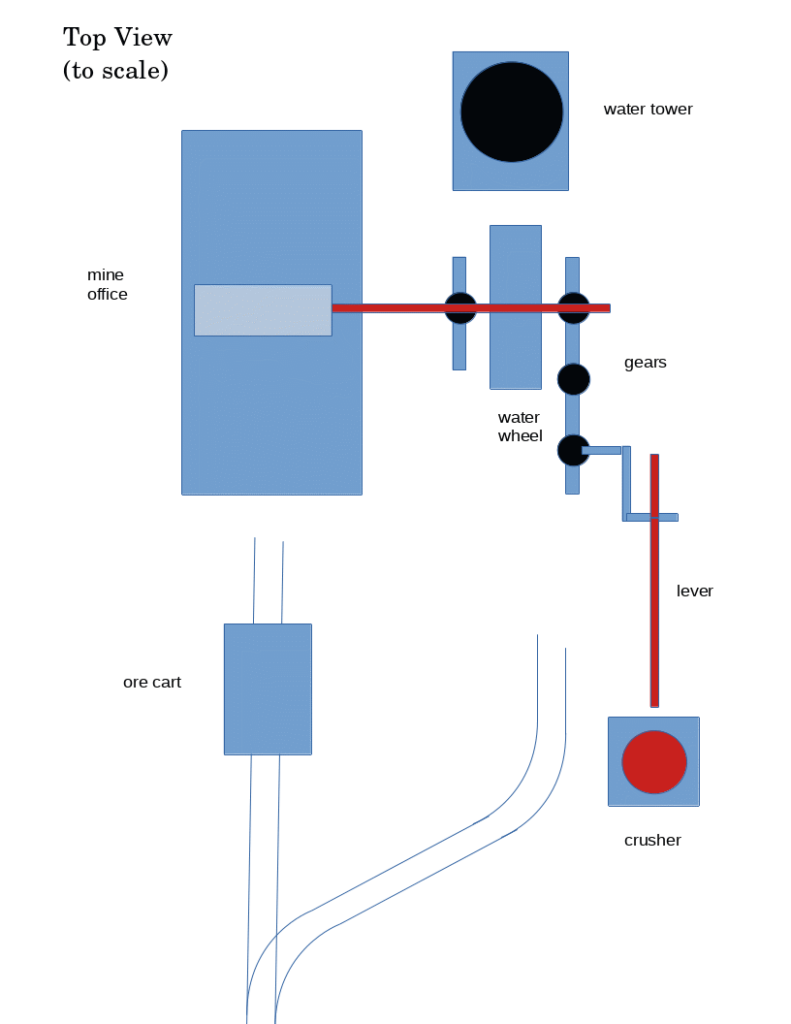
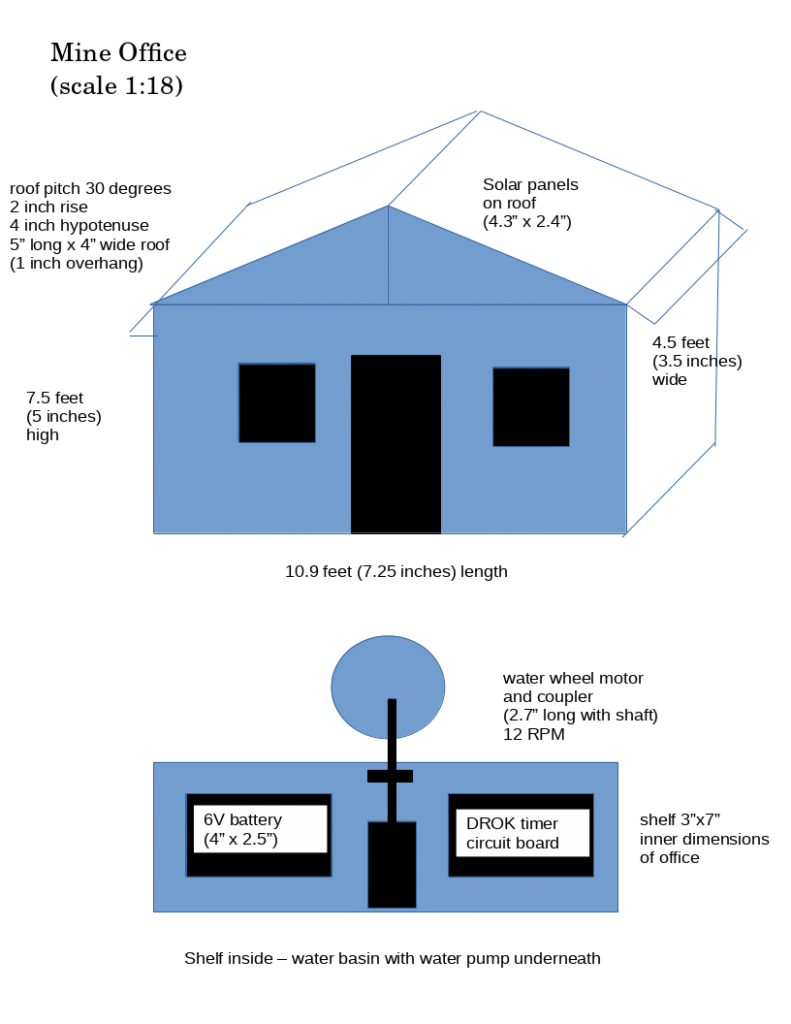
The mechanics and electronics will be hidden inside the mine office. The roof will be removable to give access the interior of the structure.

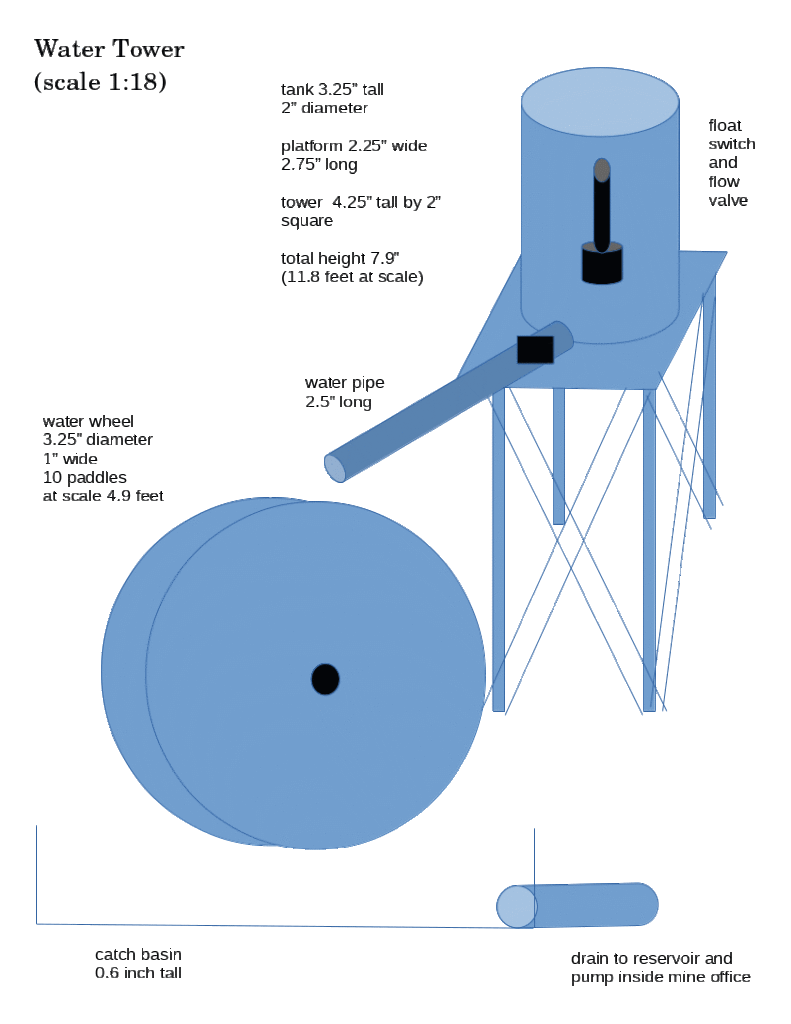
The water pump will be submerged in a reservoir in the bottom of the mine office. Water will be pumped up into the water tower. A float switch inside the water tower will start and stop the pump so that the tower does not overflow. Water will drain out of the tower through a pipe. A screw type flow valve will be constructed to adjust the release flow.

The water from the water wheel will be collected underneath the wheel and gravity fed into the reservoir in the mine office.

I need to calculate the charge rate and current draw of the pump and motor to verify the required battery capacity and operational duty cycle.

Two 1W solar panels will be situated on the mine office roof. These panels will charge a 6V rechargeable battery inside the mine office. Output current for each solar panel is 165mA at 6V.

Rechargeable AA NiMH batteries typically have a capacity of about 2000 mAh. With two solar panels giving 330mA capacity I should be able to charge 4 AA batteries in about 8 hours.

If my water wheel motor operates at load for 20 seconds in every 80 seconds and I operate the motor for 10 minutes every hour, I should be running 7.5 crushing operations each hour. Maximum load should occur for 150 seconds each hour. This is 0.04 of an hour at 1500mA which works out to 62.5mAh. This would drain the batteries in about 32 hours operating every hour on the hour. If I only operate 8 hours a day and not 24 hours a day I may have close to 100 hours of operating time.

Given that I can charge in 8 hours and I have 100 hours of operating time I am optimistic that I will have enough capacity to operate my motor and pump, even with inefficient charging.