Yellow Brick Road – Introduction
The Yellow Brick Road is a wonderful project that is intended to mix up two stories about the Wizard of Oz and Alice in Wonderland. Each story is set in a fantasy land and has a young heroine and an evil woman antagonist. For the mathematics in this project I plan to use an Archimedes spiral that defines the start of the Yellow Brick Road. I will set Alice in Wonderland on the road as my bronze figure, and there will be a copper witches hat for the wicked witch of the East, and a brass Queen of Hearts card for the other nasty woman.
The mathematics of this work relates to an Archimedes spiral. This type of spiral is drawn by continually moving outwards from the center as you draw a circle. The spiral is the set of points that correspond to the locations over time of a point moving away from a fixed point with a constant speed along a line which rotates with constant angular velocity. Equivalently, in polar coordinates (r, θ) it can be described by the equation
with real numbers a and b. Changing the parameter a will turn the spiral, while b controls the distance between successive turnings. There is a video describing how to draw an Archimedes Spiral here .
 Yellow Brick Road
Yellow Brick Road
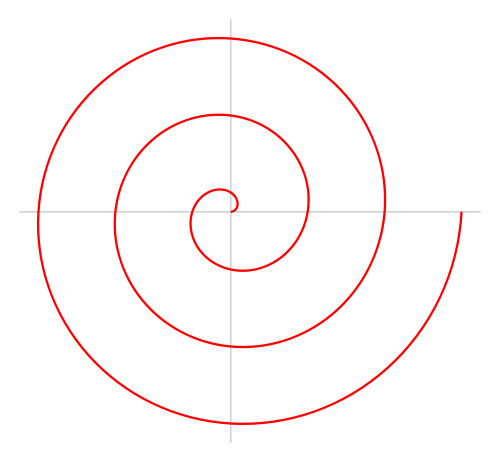 Archimedean Spiral
Archimedean Spiral
Alice is a curious figure. She will be standing on the Yellow Brick Road looking somewhat apprehensive or pensive about her pending journey. On the other side of the road I will set the witches hat and the Queen of Hearts card to portray each of the evil antagonists in the tales.
 Alice in Wonderland
Alice in Wonderland

Alice in Wonderland
The witches hat is another interesting mathematical construction. The hat is essentially a cone that fits inside a brim that must be fabricated at the correct size. For a 1/8 scale figure we can measure that the hat size must be a 3/4 inch diameter circle. A full brim would be 1 1/2 inches in diameter, and this would also be the height of the cone.
If we drop a perpendicular down from the top of the cone we will have a right triangle from which we can calculate the length of the hypotenuse, or the cone side.
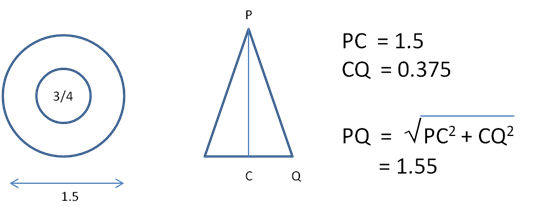
Now, if you have a cone and cut it by a line perpendicular to the circular base and then lay it out flat, you will have a sector of a circle.

We know the length of the cone side or the radius of the sector is 1.55 from above. And we know that the cone circle or brim has a radius of 0.375. And we also know from our high school math that the circumference of a circle is 2Πr.
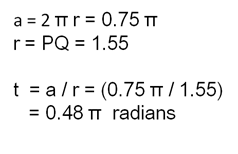
If we now multiply by 180 / Π to convert radians to degrees, this gives 87 degrees. So we now draw an arc with a radius of 1.55 and measure an angle of 87 degrees. If this segment is cut out and formed into a cone it will have the correct height and circumference to fit the hat brim.
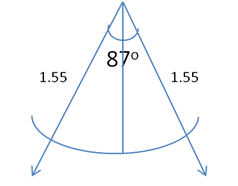
The next step is to draw out the Archimedes spiral on paper and the witches hat, too, and fabricate the design. We can then build a model of the work.


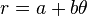

No comments yet.